[几何] 前几天粉丝群里的一几何题

(85.61 KB)

2012-11-15 19:23

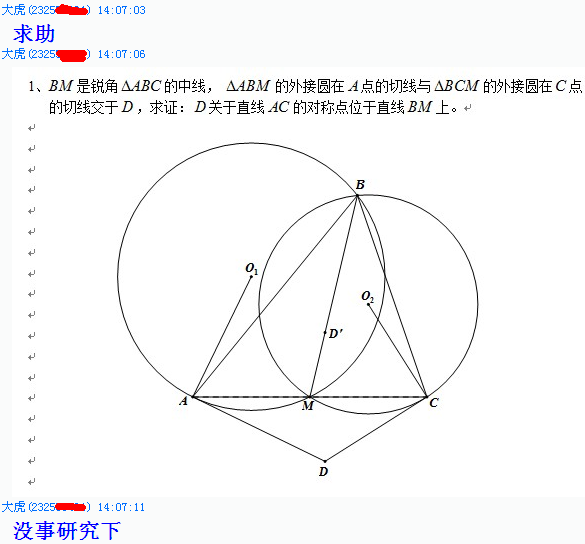
题目：$BM$ 是锐角 $\triangle ABC$ 的中线，$\triangle ABM$ 的外接圆在 $A$ 点的切线与 $\triangle BCM$ 的外接圆在 $C$ 点的切线交于 $D$。
求证：$D$ 关于直线 $AC$ 的对称点位于直线 $BM$ 上。

证明：在 $BM$ 上取一点 $E$，使 $ME\cdot MB=(AC/2)^2$，此时易证
\begin{align*}
\triangle MEA &\sim \triangle MAB,\\
\triangle MEC &\sim \triangle MCB,
\end{align*}
所以有
\begin{align*}
\angle MAE &= \angle MBA = \angle MAD,\\
\angle MCE &= \angle MBC = \angle MCD,
\end{align*}
可见 $E$ 和 $D$ 关于 $AC$ 对称，故得证。

ME⋅MB=(AC/2)^2

看到这个就想到反演，不过，都快忘记了……