[不等式] 来自人教数学群的三元不等式想切线

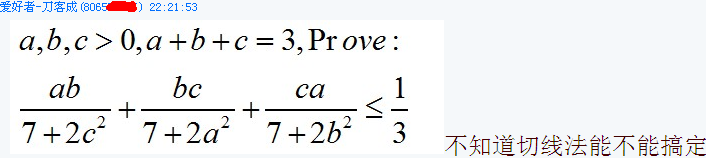
(47.5 KB)

2012-10-30 15:36

群里后面提到，想先均值放缩再切线，结果会反向，而用切平面也失败。
后来我想到用局部切线，先不管 $ab$，只切 $1/(7+2c^2)$，结果切直线和抛物线均失败，然后就睡觉去了，决定睡醒后上软件暴力切三次函数试试，结果刚才居然切成功了，不过真的挺暴力，不用软件我不敢算。

题目：已知 $a$, $b$, $c>0$ 且 $a+b+c=3$，求证
\[\frac{ab}{7+2c^2}+\frac{bc}{7+2a^2}+\frac{ca}{7+2b^2}\leqslant \frac13.\]

证明：我们先证明对任意的 $x\geqslant 0$ 都有
\begin{equation}\label{20121030baoliqie}
\frac{567}{7+2x^2}\leqslant K(x),
\end{equation}
其中
\[K(x)=4x^3-18x^2-4x+81+9\sqrt{\frac27}(x-1)^2x,\]
事实上，作差因式分解有
\[K(x)-\frac{567}{7+2x^2}=\frac{\bigl( 28+9\sqrt{14} \bigr)\bigl( 9\sqrt{14}-28-10x \bigr)^2(x-1)^2x}{350(2x^2+7)}\geqslant 0,\]
所以式 \eqref{20121030baoliqie} 成立。

由此可见，要证原不等式，只要证明
\[abK(c)+bcK(a)+caK(b)\leqslant 189,\]
即
\begin{equation}\label{20121030zyzs1}
abc\sum\left( 4a^2-18a-4+9\sqrt{\frac27}(a-1)^2 \right)+81\sum ab\leqslant 189,
\end{equation}
由于 $0<\sum ab\leqslant \left(\sum a\right)^2/3=3$，我们可以设
\[\sum ab=3-\frac{q^2}3,\]
其中 $3>q\geqslant 0$，那么式 \eqref{20121030zyzs1} 可以化简为
\begin{equation}\label{20121030zyzs2}
2abc\left( 3q^2\sqrt{\frac27}+\frac{4q^2}3-27 \right)+27(2-q^2)\leqslant 0,
\end{equation}
易证 $3q^2\sqrt{2/7}+4q^2/3-27<0$，于是由 pqr 定理，有
\begin{align*}
& 2abc\left( 3q^2\sqrt{\frac27}+\frac{4q^2}3-27 \right)+27(2-q^2) \\
\leqslant{}& \frac{2(3+q)^2(3-2q)}{27}\left( 3q^2\sqrt{\frac27}+\frac{4q^2}3-27 \right)+27(2-q^2) \\
={}&\frac{-q^2}{567}\left( \bigl( 112+36\sqrt{14} \bigr)q^3+\bigl( 504+162\sqrt{14} \bigr)q^2-2268q-486\sqrt{14}+3591 \right),
\end{align*}
可以证明 $\bigl( 112+36\sqrt{14} \bigr)q^3+\bigl( 504+162\sqrt{14} \bigr)q^2-2268q-486\sqrt{14}+3591>0$，所以式 \eqref{20121030zyzs2} 成立，原不等式得证。

好暴力........又是个非暴力不合作的
不愧是K版，连函数都是 $K(x)$..........

1# kuing


好暴力啊，有没有简单点的？

好暴力........又是个非暴力不合作的
不愧是K版，连函数都是 $K(x)$..........
都市侠影 发表于 2012-10-30 16:16

故意用K的

1# kuing

好暴力啊，有没有简单点的？
pxchg1200 发表于 2012-10-30 16:16

暂时没想到，CS、AG什么的技术靠你们了，那些我还没掌握。

补充最后“可以证明”的证明
\begin{align*}
&\bigl( 112+36\sqrt{14} \bigr)q^3+\bigl( 504+162\sqrt{14} \bigr)q^2-2268q-486\sqrt{14}+3591\\
={}&\left(4 \bigl(28+9 \sqrt{14}\bigr) q+\frac65 \bigl(28+9 \sqrt{14}\bigr) \left(5+2 \sqrt{54 \sqrt{14}-143}\right)\right) \left(q-\frac3{10} \left(\sqrt{54 \sqrt{14}-143}-5\right)\right)^2\\
&+\frac{27}5 \left(1435-45 \sqrt{14}-\sqrt{450324 \sqrt{14}-431858}\right),
\end{align*}
其中 $1435-45 \sqrt{14}-\sqrt{450324 \sqrt{14}-431858}\approx 147.20587$，所以……