[不等式] 来自pep的求加强为非严格不等式

来自 http://bbs.pep.com.cn/thread-1965360-1-1.html

谁能把这个严格不等式加强为非严格不等式？
《数学通报》2011年4月号问题

加强为如下不等式，很平凡的 $a=b=c=1/3$ 取等，证法也很平凡。
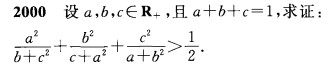
$a,b,c\in\mathbb{R}^+$，$a+b+c=1$，则
\[\frac{a^2}{b+c^2}+\frac{b^2}{c+a^2}+\frac{c^2}{a+b^2}\geqslant \frac34.\]

证  齐次化为
\[\frac{a^2}{b(a+b+c)+c^2}+\frac{b^2}{c(a+b+c)+a^2}+\frac{c^2}{a(a+b+c)+b^2}\geqslant \frac34,\]
由柯西不等式有
\[\sum{\frac{a^2}{b(a+b+c)+c^2}}\geqslant \frac{\left( \sum{a^2} \right)^2}{\sum{\bigl(a^2b(a+b+c)+a^2c^2\bigr)}},\]
故只要证
\[4\left( \sum{a^2} \right)^2\geqslant 3\sum{\bigl(a^2b(a+b+c)+a^2c^2\bigr)},\]
展开整理为
\[3\left( \sum{a^{4}}-\sum{a^{3}b} \right)+\left( \sum{a^2} \right)^2-abc\sum{a}\geqslant 0,\]
显然成立，得证。

1# kuing

\[4\left( \sum{a^2} \right)^2\geqslant 3\sum{\bigl(a^2b(a+b+c)+a^2c^2\bigr)}, \]
其实不用展开了，kk

by Vasc inequality:
\[ (a^{2}+b^{2}+c^{2})^{2}\geq 3(a^{3}b+b^{3}c+c^{3}a) \]
and
\[ (a^{2}+b^{2}+c^{2})^{2}\geq 3(a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2})\geq 2(a^{2}b^{2}+b^{2}c^{2}+c^{2}a^{2})+(a^{2}bc+b^{2}ac+c^{2}ab) \]
第二个乘个3加上第一个得证！

另外，这个呢？
设正数$a,b,c$ 有$a+b+c=3$ 证明：
\[ \frac{a}{\sqrt{b+c^{2}}}+\frac{b}{\sqrt{c+a^{2}}}+\frac{c}{\sqrt{a+b^{2}}}\geq \frac{3}{\sqrt{2}} \]

我觉得很像那个啊。
（今年都不去Mathlink了，所以跑这里来玩。）

2# pxchg1200

展开其实也没多少功夫，目测即可
再说，能用简单的不等式就用简单的，说vasc不等式，那贴楼主还不知了不了解，呵呵。

3# pxchg1200


设正数$a,b,c$满足$a+b+c=3$,则对任意$k\geq 0$,证明
\[\frac{a}{\sqrt{kb+c^2}}+\frac{b}{\sqrt{kc+a^2}}+\frac{c}{\sqrt{ka+b^2}}\geq \frac{3}{\sqrt{k+1}}\]