|
1#
|
|
|
|
|
2#
|
|
|
|
|
3#
|
|
|
|
|
4#
|
|
|
|
|
5#
|
|
|
|
||
|
6#
|
|
|
|
|
7#
|
|
|
|
||
|
8#
|
|
|
|
|
9#
|
|
|
|
||
|
10#
|
|
|
|
|
11#
|
|
|
|
||
|
12#
|
|
|
|
|
13#
|
|
|
|
||
|
14#
|
|
|
|
|
15#
|
|
|
|
||
|
16#
|
|
|
|
|
17#
|
|
|
|
|
18#
|
|
|
|
|
19#
|
|
|
|
|
20#
|
|
|
|

 发表于 2013-3-23 17:19
发表于 2013-3-23 17:19
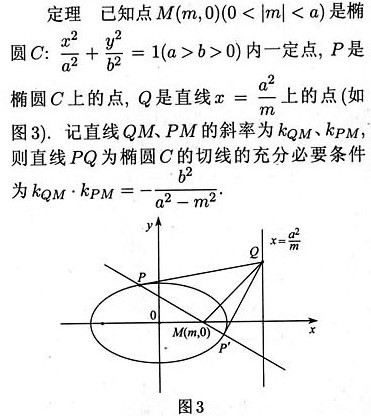
 发表于 2013-3-24 00:02
发表于 2013-3-24 00:02
 代码的各种好处……
代码的各种好处……