抄来的(代码自己打的):设 $\veps=\cos(2\pi/n)+i\sin(2\pi/n)$,则 $x^n=1$ 的所有根为 $1$, $\veps$, $\veps^2$, $\ldots$, $\veps^{n-1}$,所以
\[x^n-1=(x-1)(x-\veps)(x-\veps^2)\cdots(x-\veps^{n-1}),\]
又
\[x^n-1=(x-1)(x^{n-1}+x^{n-2}+\cdots+1),\]
所以
\[x^{n-1}+x^{n-2}+\cdots+1=(x-\veps)(x-\veps^2)\cdots(x-\veps^{n-1}),\]
上式令 $x=1$ 得
\[(1-\veps)(1-\veps^2)\cdots(1-\veps^{n-1})=n,\]
取模得
\[\abs{1-\veps}\abs{1-\veps^2}\cdots\abs{1-\veps^{n-1}}=n,\]
由隶莫佛公式有
\begin{align*}
\abs{1-\veps^k}&=\abs{1-\cos\frac{2k\pi}n-i\sin\frac{2k\pi}n}\\
&=\sqrt{\left(1-\cos\frac{2k\pi}n\right)^2+\sin^2\frac{2k\pi}n}\\
&=\sqrt{2-2\cos\frac{2k\pi}n}\\
&=2\abs{\sin\frac{k\pi}n},
\end{align*}
于是
\[\abs{1-\veps}\abs{1-\veps^2}\cdots\abs{1-\veps^{n-1}}=2^{n-1}\sin\frac\pi n\sin\frac{2\pi}n\cdots\sin\frac{(n-1)\pi}n,\]
即得
\[\sin\frac\pi n\sin\frac{2\pi}n\cdots\sin\frac{(n-1)\pi}n=\frac n{2^{n-1}}.\] |

 发表于 2013-3-16 20:28
发表于 2013-3-16 20:28
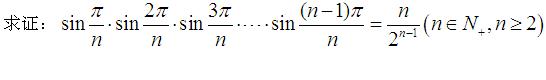
 发表于 2013-3-16 20:33
发表于 2013-3-16 20:33