|
1#
|
|
|
|
||
|
2#
|
|
|
|
||
|
3#
|
|
|
|
|
4#
|
|
|
|
||
|
5#
|
|
|
|
||
|
6#
|
|
|
|
||
|
7#
|
|
|
|
||
|
8#
|
|
|
|
||
|
9#
|
|
|
|
||
|
10#
|
|
|
|
||
|
11#
|
|
|
|
|
12#
|
|
|
|
||

 发表于 2013-3-12 22:57
发表于 2013-3-12 22:57
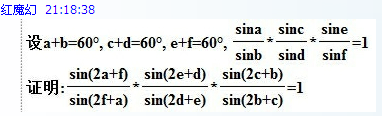
 还是不会
还是不会
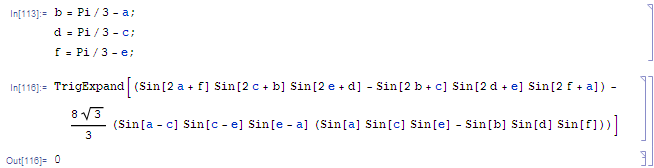
 发表于 2013-3-15 20:39
发表于 2013-3-15 20:39
 你们自己可以推一下……
你们自己可以推一下……
 没人鸟……
没人鸟……
