[不等式] 来自人教群的小题（04-05法国竞赛题）

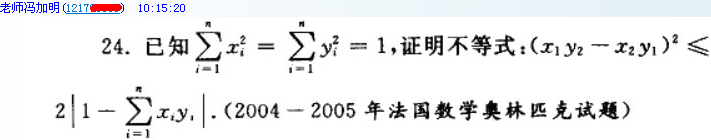
(47.2 KB)

2013-2-24 10:50

老师冯加明(1217*****)
24. 已知 $\sum_{i=1}^n x_i^2=\sum_{i=1}^n y_i^2=1$，证明不等式
\[(x_1y_2-x_2y_1)^2\leqslant 2\left|1-\sum_{i=1}^n x_iy_i\right|.\]
（2004-2005 年法国数学奥林匹克试题）

由拉格朗日恒等式以及柯西不等式得
\begin{align*}
(x_1y_2-x_2y_1)^2&\leqslant \sum_{1\leqslant i<j\leqslant n}{(x_iy_j-x_jy_i)^2} \\
& =\sum x_i^2\sum y_i^2-\left( \sum x_iy_i \right)^2 \\
& =\left| 1-\sum x_iy_i \right|\cdot \left| 1+\sum x_iy_i \right| \\
& \leqslant \left| 1-\sum x_iy_i \right|\left( 1+\left| \sum x_iy_i \right| \right) \\
& \leqslant \left| 1-\sum x_iy_i \right|\left( 1+\sqrt{\sum x_i^2\sum y_i^2} \right) \\
& =2\left| 1-\sum x_iy_i \right|.
\end{align*}

待证不等式左边居然只有一项，而不是循环和！
过分了噻