|
1#
|
|
|
|
||
|
2#
|
|
|
|
||
|
3#
|
|
|
|
|
4#
|
|
|
|
|
5#
|
|
|
|
||
|
6#
|
|
|
|
|
7#
|
|
|
|
||
|
8#
|
|
|
|
||
|
9#
|
|
|
|
|
10#
|
|
|
|
||
|
11#
|
|
|
|
|
12#
|
|
|
|
||
|
13#
|
|
|
|
|
14#
|
|
|
|
||
|
15#
|
|
|
|
|
16#
|
|
|
|
||
|
17#
|
|
|
|
|
18#
|
|
|
|
|
19#
|
|
|
|
||
|
20#
|
|
|
|

 发表于 2013-2-2 15:50
发表于 2013-2-2 15:50
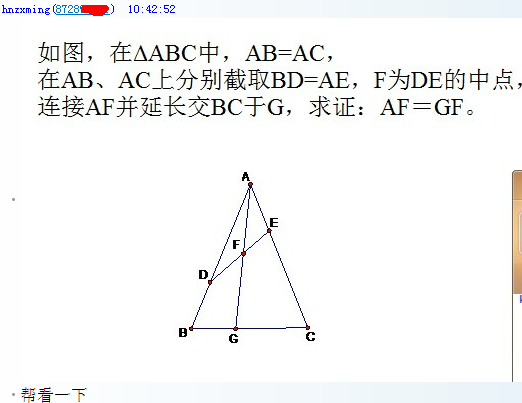
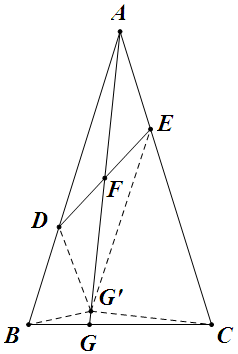
 ……但总感觉可行……
……但总感觉可行……
 发表于 2013-2-2 18:42
发表于 2013-2-2 18:42

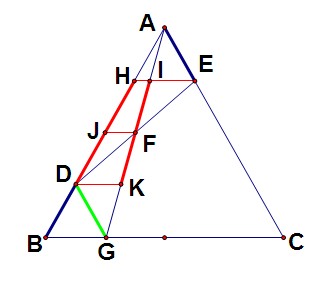

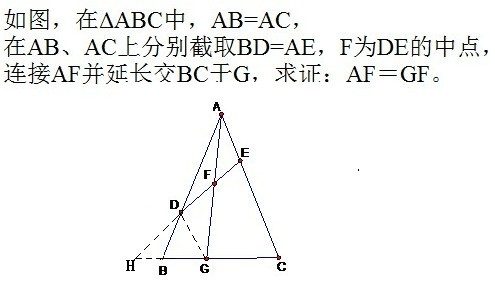
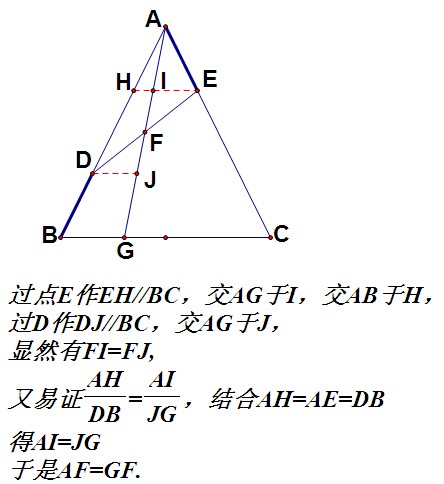
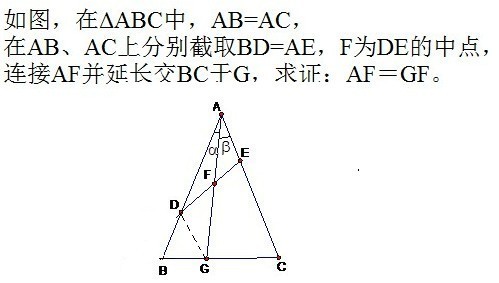
 ,谢谢
,谢谢