[不等式] 来自某教师群的一道绝对值不等式求参数范围

(11.07 KB)

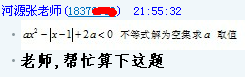
2013-1-7 22:33

字有点小，而且后面漏了“范围”二字，我重新打一打：

若关于 $x$ 的不等式 $ax^2-\abs{x-1}+2a<0$ 的解集为空集，求 $a$ 的取值范围。

解：分离变量有
\[ax^2-\abs{x-1}+2a<0\iff a<\frac{\abs{x-1}}{x^2+2}=f(x),\]
下面求 $f(x)$ 的最大值，由均值不等式，有
\begin{align*}
f(x)&=\frac{\abs{x-1}}{(x-1)^2+3+2(x-1)} \\
& \leqslant \frac{\abs{x-1}}{(x-1)^2+3-2\abs{x-1}} \\
& =\frac1{\abs{x-1}+\dfrac3{\abs{x-1}}-2} \\
& \leqslant \frac1{2\sqrt3-2}=\frac{\sqrt3+1}4,
\end{align*}
当 $x=1-\sqrt3$ 时等号成立，故 $f(x)$ 的最大值就是
\[f(x)_{\max}=f\bigl(1-\sqrt3\bigr)=\frac{\sqrt3+1}4,\]
所以要原不等式解集为空，只需 $a\geqslant \frac{\sqrt3+1}4$。

一次就成功了，还不需要讨论去绝对值，放缩等号也能同时取到，妙！

显然a>0，故原不等式可化为x^2+2>=|x-1|/a恒成立，做出两个函数图像，发现x<1时相切时，可以得到1/a的最大值，于是可得到a的最小值

(19.27 KB)

2013-1-7 23:48

3# yes94

嗯，图象法也不错。

目前只能搞这种高考的了，
再来一种：

(29.53 KB)

2013-1-8 00:16

最后分母有理化失误，答案的分子是加号。
取等号条件同版主的，这里略去